—————线性表、栈—————
线性表 1 2 3 4 5 6 7 8 9 10 11 class SqList { private final int MAXSIZE = 100 ; private int [] data = new int [MAXSIZE]; private int length; } class ListNode { int val; ListNode next; ListNode prev; }
反转数组 1 2 3 4 5 6 7 8 9 public void reverseSqList (int [] arr) { int left = 0 ; int right = arr.length - 1 ; while (left < right) { swap(data[left], data[right]); left++; right--; } }
反转链表 反转一个单链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 public ListNode reverseLinkList (ListNode head) { ListNode prev = null ; ListNode curr = head; ListNode next; while (curr != null ) { next = curr.next; curr.next = prev; prev = curr; curr = next; } return prev; }
合并两个数组 合并两个有序数组为一个有序数组。
1 2 3 4 5 6 7 8 9 10 11 12 13 public void merge (int [] nums1, int m, int [] nums2, int n) { int i = m - 1 , j = n - 1 , k = m + n - 1 ; while (i >= 0 && j >= 0 ) { if (nums1[i] > nums2[j]) { nums1[k--] = nums1[i--]; } else { nums1[k--] = nums2[j--]; } } while (j >= 0 ) { nums1[k--] = nums2[j--]; } }
合并两个链表 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public static ListNode mergeTwoLists (ListNode l1, ListNode l2) { ListNode dummy = new ListNode (0 ); ListNode current = dummy; while (l1 != null && l2 != null ) { if (l1.val < l2.val) { current.next = l1; l1 = l1.next; } else { current.next = l2; l2 = l2.next; } current = current.next; } if (l1 != null ) { current.next = l1; } else { current.next = l2; } return dummy.next; }
拆分两个数组 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static void splitArray (int [] inputArray) { List<Integer> oddNumbers = new ArrayList <>(); List<Integer> evenNumbers = new ArrayList <>(); for (int num : inputArray) { if (num % 2 == 0 ) { evenNumbers.add(num); } else { oddNumbers.add(num); } } int [] oddArray = oddNumbers.stream().mapToInt(Integer::intValue).toArray(); int [] evenArray = evenNumbers.stream().mapToInt(Integer::intValue).toArray(); }
拆分两个链表 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public static ListNode[] splitListToParts(ListNode head) { ListNode oddDummy = new ListNode (0 ); ListNode evenDummy = new ListNode (0 ); ListNode oddCurrent = oddDummy; ListNode evenCurrent = evenDummy; ListNode current = head; int index = 1 ; while (current != null ) { if (index % 2 == 1 ) { oddCurrent.next = current; oddCurrent = oddCurrent.next; } else { evenCurrent.next = current; evenCurrent = evenCurrent.next; } current = current.next; index++; } oddCurrent.next = null ; evenCurrent.next = null ; return new ListNode []{oddDummy.next, evenDummy.next}; }
TopK 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public static int [] findTopKElements(int [] data, int k) { PriorityQueue<Integer> minHeap = new PriorityQueue <>(k); for (int num : data) { if (minHeap.size() < k) { minHeap.offer(num); } else { if (num > minHeap.peek()) { minHeap.poll(); minHeap.offer(num); } } } int [] result = new int [k]; int index = 0 ; while (index < k) result[index++] = minHeap.poll(); return result; } public static int [] findTopK(int [] nums, int k) { Arrays.sort(nums); int [] result = new int [k]; System.arraycopy(nums, nums.length - k, result, 0 , k); return result; }
数组和列表之间的转换 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public static void testArray2List () { String[] strs = {"aaa" ,"bbb" ,"ccc" }; List<String> list = Arrays.asList(strs); for (String s : list) { System.out.println(s); } } public static void testList2Array () { List<String> list = new ArrayList <String>(); list.add("aaa" ); list.add("bbb" ); list.add("ccc" ); String[] array = list.toArray(new String [list.size()]); for (String s : array) { System.out.println(s); } }
栈、队列 用栈实现队列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public class QueueWithTwoStacks { private Stack<Integer> stackA; private Stack<Integer> stackB; public 用两个栈实现队列_QueueWithTwoStacks() { stackA = new Stack <>(); stackB = new Stack <>(); } public void enqueue (int value) { stackA.push(value); } public int dequeue () { if (stackB.isEmpty()) { while (!stackA.isEmpty()) { stackB.push(stackA.pop()); } } return stackB.pop(); } public boolean isEmpty () { return stackA.isEmpty() && stackB.isEmpty(); } public int size () { return stackA.size() + stackB.size(); } public static void main (String[] args) { QueueWithTwoStacks queue = new QueueWithTwoStacks (); System.out.println(queue.isEmpty()); queue.enqueue(1 ); queue.enqueue(2 ); queue.enqueue(3 ); System.out.println(queue.dequeue()); System.out.println(queue.dequeue()); queue.enqueue(4 ); System.out.println(queue.dequeue()); queue.enqueue(5 ); queue.enqueue(6 ); System.out.println(queue.size()); System.out.println(queue.isEmpty()); } }
用数组实现循环队列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public class CircularQueue { private int [] queue; private int front; private int rear; private int capacity; public CircularQueue (int capacity) { this .capacity = capacity; queue = new int [capacity]; front = 0 ; rear = -1 ; } public boolean enqueue (int value) { if (isFull()) { return false ; } rear = (rear + 1 ) % capacity; queue[rear] = value; return true ; } public int dequeue () { if (isEmpty()) { throw new IllegalStateException ("Queue is empty." ); } int value = queue[front]; front = (front + 1 ) % capacity; return value; } public boolean isEmpty () { return front == 0 && rear == -1 ; } public boolean isFull () { return (rear + 1 ) % capacity == front; } }
判断字符串中的括号是否有效配对。例如[]{()()}}。
1 2 3 4 5 6 7 8 9 10 11 public boolean isValid (String s) { Stack<Character> stack = new Stack <>(); for (char ch : s.toCharArray()){ if (ch == '(' ) stack.push(')' ); else if (ch == '[' ) stack.push(']' ); else if (ch == '{' ) stack.push('}' ); else if (stack.isEmpty() || stack.pop() != ch) return false ; } return stack.isEmpty(); }
最小栈 设计一个可以获取最小元素的栈。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class MinStack { private Stack<Integer> stack; private Stack<Integer> minStack; public MinStack () { stack = new Stack <>(); minStack = new Stack <>(); } public void push (int val) { stack.push(val); if (minStack.isEmpty() || val <= minStack.peek()) { minStack.push(val); } } public void pop () { if (stack.pop().equals(minStack.peek())) { minStack.pop(); } } public int top () { return stack.peek(); } public int getMin () { return minStack.peek(); } }
———————树———————
二叉树 二叉树结构 1 2 3 4 5 6 7 8 class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } }
前序|中序|后序、层次遍历 实现二叉树的前序、中序、后序、层次遍历。
1 2 3 4 5 6 7 8 private static void preOrder (BinaryNode<Integer> root) { if (root != null ) { System.out.print(root.val + " " ); preOrder(root.left); preOrder(root.right); } }
1 2 3 4 5 6 7 8 private static void inOrder (BinaryNode<Integer> root) { if (root != null ) { inOrder(root.left); System.out.print(root.val + " " ); inOrder(root.right); } }
1 2 3 4 5 6 7 8 private static void postOrder (BinaryNode<Integer> root) { if (root != null ) { postOrder(root.left); postOrder(root.right); System.out.print(root.val + " " ); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static List<List<Integer>> levelOrder (BinaryNode<Integer> root) { List<List<Integer>> result = new ArrayList <>(); if (root == null ) { return result; } Queue<BinaryNode<Integer>> queue = new LinkedList <>(); queue.add(root); while (!queue.isEmpty()) { List<Integer> level = new ArrayList <>(); int size = queue.size(); for (int i = 0 ; i < size; i++) { BinaryNode<Integer> node = queue.poll(); level.add(node.val); if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } result.add(level); } return result; }
查找、插入、删除、更新 1 2 3 4 5 6 7 8 9 10 11 12 public static BinaryNode<Integer> search (BinaryNode<Integer> root, int key) { if (root == null || root.val == key) { return root; } if (key < root.val) { return search(root.left, key); } else { return search(root.right, key); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public static BinaryNode<Integer> insert (BinaryNode<Integer> root, int data) { if (root == null ) { return new BinaryNode <>(data); } if (data <= root.val) { root.left = insert(root.left, data); } else { root.right = insert(root.right, data); } return root; } public static void insertBatch (BinaryNode<Integer> root, List<Integer> datas) { datas.forEach(data -> insert(root, data)); } public static void insertBatch (BinaryNode<Integer> root, int [] datas) { insertBatch(root, Arrays.stream(datas).boxed().toList()); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public static BinaryNode<Integer> delete (BinaryNode<Integer> root, int key) { if (root == null ) { return null ; } if (key < root.val) { root.left = delete(root.left, key); } else if (key > root.val) { root.right = delete(root.right, key); } else { if (root.left == null ) { return root.right; } else if (root.right == null ) { return root.left; } root.val = searchMin(root.right).val; root.right = delete(root.right, root.val); } return root; } private static BinaryNode<Integer> searchMin (BinaryNode<Integer> root) { while (root.left != null ) { root = root.left; } return root; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public static BinaryNode<Integer> update (BinaryNode<Integer> root, Integer key, Integer val) { if (root == null ) { return null ; } if (key < root.val) { root.left = update(root.left, key, val); } else if (key > root.val) { root.right = update(root.right, key, val); } else { root.val = val; } return root; }
翻转二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 public static BinaryNode<Integer> invertTree (BinaryNode<Integer> root) { if (root == null ) { return null ; } BinaryNode<Integer> temp = root.left; root.left = invertTree(root.right); root.right = invertTree(temp); return root; }
判断路径总和 判断二叉树中是否存在一条路径,其路径和等于给定的数值。
1 2 3 4 5 public boolean hasPathSum (TreeNode root, int sum) { if (root == null ) return false ; if (root.left == null && root.right == null ) return sum == root.val; return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val); }
判断镜像二叉树 判断一个二叉树是否是它的镜像。
1 2 3 4 5 6 7 8 9 10 11 12 public boolean isSymmetric (TreeNode root) { if (root == null ) return true ; return isMirror(root.left, root.right); } private boolean isMirror (TreeNode t1, TreeNode t2) { if (t1 == null && t2 == null ) return true ; if (t1 == null || t2 == null ) return false ; return (t1.val == t2.val) && isMirror(t1.right, t2.left) && isMirror(t1.left, t2.right); }
哈夫曼树 哈夫曼编码原理 哈夫曼树结构 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class HuffmanNode <T> extends BinaryNode <T> implements Comparable <HuffmanNode<T>> { public T val; public HuffmanNode<T> left; public HuffmanNode<T> right; public int frequency; public HuffmanNode (T val, int frequency) { super (val); this .val = val; this .frequency = frequency; } public HuffmanNode (HuffmanNode<T> left, HuffmanNode<T> right) { super (null , left, right); this .val = null ; this .frequency = left.frequency + right.frequency; } public HuffmanNode (T val, HuffmanNode<T> left, HuffmanNode<T> right) { super (val, left, right); this .val = val; this .left = left; this .right = right; this .frequency = left.frequency + right.frequency; } @Override public int compareTo (HuffmanNode<T> other) { return Integer.compare(this .frequency, other.frequency); } }
构建哈夫曼树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static Map<Character, Integer> calculateFrequencies (String str) { Map<Character, Integer> frequencies = new HashMap <>(); for (char ch : str.toCharArray()) { frequencies.put(ch, frequencies.getOrDefault(ch, 0 ) + 1 ); } return frequencies; } public static HuffmanNode<Character> buildHuffmanTree (Map<Character, Integer> frequencies) { PriorityQueue<HuffmanNode<Character>> priorityQueue = new PriorityQueue <>(); for (Map.Entry<Character, Integer> entry : frequencies.entrySet()) { priorityQueue.offer(new HuffmanNode <>(entry.getKey(), entry.getValue())); } while (priorityQueue.size() > 1 ) { HuffmanNode<Character> left = priorityQueue.poll(); HuffmanNode<Character> right = priorityQueue.poll(); int mergedFrequency = left.frequency + right.frequency; HuffmanNode<Character> mergedNode = new HuffmanNode <>(null , mergedFrequency); mergedNode.left = left; mergedNode.right = right; priorityQueue.offer(mergedNode); } return priorityQueue.poll(); }
哈夫曼编码、解码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static Map<Character, String> encode ( HuffmanNode<Character> node, String code, Map<Character, String> codes ) { if (node != null ) { if (node.val != null ) { codes.put(node.val, code); } else { generateCodes(node.left, code + "0" , codes); generateCodes(node.right, code + "1" , codes); } } return codes; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public static String decode (HuffmanNode<Character> root, String encodedString) { StringBuilder decodedString = new StringBuilder (); HuffmanNode<Character> currentNode = root; for (char bit : encodedString.toCharArray()) { currentNode = (bit == '0' ) ? currentNode.left : currentNode.right; if (currentNode.val != null ) { decodedString.append(currentNode.val); currentNode = root; } } return decodedString.toString(); }
计算带权路径长度、压缩率 1 2 3 4 5 6 7 8 9 public static int calculateWPL (HuffmanNode<Character> node, int depth) { if (node == null ) { return 0 ; } if (node.val != null ) { return node.frequency * depth; } return calculateWPL(node.left, depth + 1 ) + calculateWPL(node.right, depth + 1 ); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public static int calculateOriginalSize (String str) { return str.length() * Character.SIZE; } public static int calculateEncodedSize (String encodedString) { return encodedString.length(); } public static double calculateCompressionRate (int originalSize, int encodedSize) { return (1 - (double ) encodedSize / originalSize) * 100 ; }
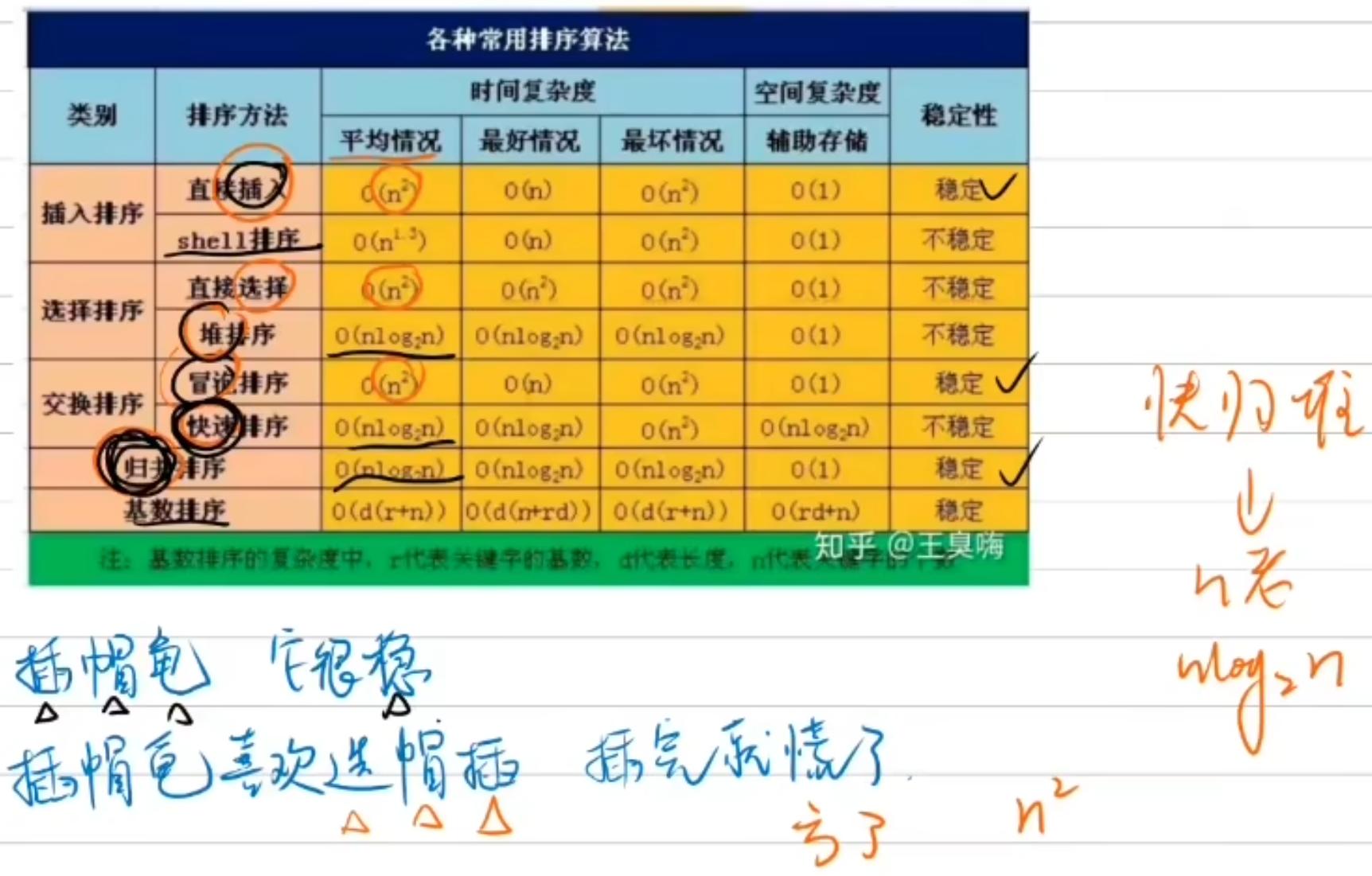
————-排序、搜索算法————-
排序算法 交换算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 private void swap (int [] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } private void swap (int a, int b) { a = a + b; b = a - b; a = a - b; }
插入类排序 在插入排序时,使用二分查找找到插入的位置,从而减少比较次数(但仍然需要线性时间插入元素)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public static void InsertSort (int [] R) { int i, j, temp; for (i = 1 ; i < R.length; i++) { temp = R[i]; for (j = i - 1 ; j >= 0 ; j--) { if (temp < R[j]){ R[j + 1 ] = R[j]; } else { break ; } } R[j + 1 ] = temp; } }
选择类排序 在选择最小元素时,记录最小元素的索引,并在每次找到更小元素时更新索引。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public static void SelectSort (int [] R) { int i, j, k, temp; for (i = 0 ; i < R.length; i++) { k = i; for (j = i + 1 ; j < R.length; j++) { if (R[j] < R[k]) { k = j; } } swap(R, i, k); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 public static void heapSort (int [] arr) { int n = arr.length; for (int i = n / 2 - 1 ; i >= 0 ; i--) { heapify(arr, n, i); } for (int i = n - 1 ; i > 0 ; i--) { int temp = arr[0 ]; arr[0 ] = arr[i]; arr[i] = temp; heapify(arr, i, 0 ); } } private static void heapify (int [] arr, int n, int i) { int largest = i; int left = 2 * i + 1 ; int right = 2 * i + 2 ; if (left < n && arr[left] > arr[largest]) { largest = left; } if (right < n && arr[right] > arr[largest]) { largest = right; } if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; heapify(arr, n, largest); } } public static void pushHeap (List<Integer> maxHeap, int insertElem) { int currentPos = maxHeap.size(); int parentPos = currentPos / 2 ; while (currentPos != 0 ) { if (insertElem > maxHeap.get(parentPos)) { maxHeap.set(currentPos, maxHeap.get(parentPos)); currentPos = parentPos; parentPos = currentPos / 2 ; } else { break ; } } maxHeap.set(currentPos, insertElem); }
交换类排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public void bubbleSort (int [] R) { int n = R.length; boolean swapped; for (int i = 0 ; i < n - 1 ; i++) { swapped = false ; for (int j = 0 ; j < n - i - 1 ; j++) { if (R[j] > R[j + 1 ]) { swap(arr, j, j+1 ) swapped = true ; } } if (!swapped) break ; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public void QuickSort (int R[], int low, int high) { int i = low, j = high, temp; if (low < high){ temp = R[low]; while (i < j){ while (i < j & &temp < R[j]) --j; if (i < j){ R[i] = R[j]; ++i; } while (i < j && temp > R[i]) ++i; if (i < j){ R[j] = R[i]; --j; } } R[i] = temp; QuickSort(R, low, i-1 ); QuickSort(R, i+1 , high); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public void quickSort (int [] R, int low, int high) { if (low < high) { int pivotIndex = partition(R, low, high); quickSort(R, low, pivotIndex - 1 ); quickSort(R, pivotIndex + 1 , high); } } private static int partition (int [] arr, int low, int high) { int pivot = arr[low]; int i = low, j = high; while (i < j) { while (j > i && arr[j] >= pivot) { j--; } if (j > i) { arr[i] = arr[j]; i++; } while (i < j && arr[i] <= pivot) { i++; } if (i < j) { arr[j] = arr[i]; j--; } } arr[i] = pivot; return i; }
归并类排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 public void mergeSort (int [] array, int left, int right) { if (left < right) { int middle = (left + right) / 2 ; mergeSort(array, left, middle); mergeSort(array, middle + 1 , right); merge(array, left, middle, right); } } private void merge (int [] array, int left, int middle, int right) { int leftSize = middle - left + 1 ; int rightSize = right - middle; int [] leftArray = new int [leftSize]; int [] rightArray = new int [rightSize]; System.arraycopy(array, left, leftArray, 0 , leftSize); System.arraycopy(array, middle + 1 , rightArray, 0 , rightSize); int i = 0 , j = 0 , k = left; while (i < leftSize && j < rightSize) { array[k++] = (leftArray[i] <= rightArray[j]) ? leftArray[i++] : rightArray[j++]; } while (i < leftSize) { array[k++] = leftArray[i++]; } while (j < rightSize) { array[k++] = rightArray[j++]; } }
分布类排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public static void radixSort (int [] R) { int max = Arrays.stream(R).max().getAsInt(); for (int exp = 1 ; max / exp > 0 ; exp *= 10 ) { countingSort(R, exp); } } private static void countingSort (int [] arr, int exp) { int n = arr.length; int [] output = new int [n]; int [] count = new int [10 ]; for (int j : arr) { int index = (j / exp) % 10 ; count[index]++; } for (int i = 1 ; i < 10 ; i++) { count[i] += count[i - 1 ]; } for (int i = n - 1 ; i >= 0 ; i--) { int index = (arr[i] / exp) % 10 ; output[count[index] - 1 ] = arr[i]; count[index]--; } System.arraycopy(output, 0 , arr, 0 , n); }
二分查找 1 2 3 4 5 6 7 8 9 10 11 12 13 public static int binSearch (int [] arr, int low, int high, int item) { while (low <= high) { int mid = (low + high) / 2 ; if (item < arr[mid]) { high = mid - 1 ; } else if (item > arr[mid]) { low = mid + 1 ; } else { return mid; } } return -1 ; }
搜索算法 广度优先搜索、深度优先搜索 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 public class 搜索算法_DFS_BFS { private int N; private List<List<Integer>> adjList; public 搜索算法_DFS_BFS(int n) { N = n; adjList = new LinkedList <>(); for (int i = 0 ; i < N; ++i) adjList.add(new LinkedList <>()); } public void addEdge (int v, int w) { adjList.get(v).add(w); adjList.get(w).add(v); } public void BFS (int val) { boolean [] visited = new boolean [N]; LinkedList<Integer> queue = new LinkedList <>(); visited[val] = true ; queue.add(val); while (!queue.isEmpty()) { val = queue.poll(); System.out.print(val + " " ); List<Integer> neighbors = adjList.get(val); for (Integer n : neighbors) { if (!visited[n]) { visited[n] = true ; queue.add(n); } } } } public void DFS (int val) { boolean [] visited = new boolean [N]; DFSUtil(val, visited); } private void DFSUtil (int v, boolean [] visited) { visited[v] = true ; System.out.print(v + " " ); List<Integer> neighbors = adjList.get(v); for (Integer w : neighbors) { if (!visited[w]) DFSUtil(w, visited); } } public static void main (String[] args) { 搜索算法_DFS_BFS g = new 搜索算法_DFS_BFS(14 ); g.addEdge(10 , 11 ); g.addEdge(10 , 12 ); g.addEdge(11 , 12 ); g.addEdge(12 , 10 ); g.addEdge(12 , 13 ); g.addEdge(13 , 13 ); System.out.print("深度优先搜索: " ); g.DFS(13 ); System.out.print("\n广度优先搜索: " ); g.BFS(11 ); } }
—————-数据淘汰算法—————-
LRU 算法(最近最少使用) 设计一个数据结构,实现最近最少使用缓存。
通过哈希表和双向链表实现。哈希表提供 O(1) 的查找时间,双向链表维护访问顺序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 class LRUCache <K, V> { private final int capacity; private final LinkedHashMap<K, V> cache; public LRUCache (int capacity) { this .capacity = capacity; this .cache = new LinkedHashMap <K, V>(capacity, 0.75f , true ) { protected boolean removeEldestEntry (Map.Entry<K,V> eldest) { return size() > LRUCache.this .capacity; } }; } public V get (K key) { return cache.getOrDefault(key, null ); } public void put (K key, V value) { cache.put(key, value); } public void remove (K key) { cache.remove(key); } public int size () { return cache.size(); } } class LRUCache <K, V> { private final int capacity; private final Map<K, V> map; public LRUCache (int capacity) { this .capacity = capacity; map = new LinkedHashMap <>(); } public void put (K key, V value) { if (map.containsKey(key)) { map.remove(key); map.put(key, value); return ; } map.put(key, value); if (map.size() > capacity) { map.remove(map.entrySet().iterator().next().getKey()); } } public V get (K key) { if (!map.containsKey(key)) { return null ; } V value = map.remove(key); map.put(key, value); return value; } } class Test { public static void main (String[] args) { LRUCache map = new LRUCache (5 ); map.put(4 , 44 ); map.put(1 , 11 ); map.put(2 , 22 ); map.put(3 , 33 ); map.put(7 , 77 ); map.put(5 , 55 ); map.put(8 , 88 ); map.put(6 , 66 ); map.put(1 , 111 ); map.put(6 , 666 ); System.out.println(map); Map<Integer, Integer> LRUmap = new LinkedHashMap <Integer, Integer>(10 , 0.75f , true ) { @Override protected boolean removeEldestEntry (Map.Entry eldest) { return size() > 10 ; } }; } }
LFU 算法(频率最少使用) 设计一个数据结构,实现最不经常使用缓存。
LFU 缓存需要同时记录使用频率和访问时间,通过哈希表和最小堆实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 class LFUCache { private final int capacity; private final Map<Integer, Node> cache; private final TreeMap<Integer, LinkedList<Node>> freqMap; private int minFreq = 0 ; private static class Node { int key, value, freq; Node(int key, int value) { this .key = key; this .value = value; this .freq = 1 ; } } public LFUCache (int capacity) { if (capacity <= 0 ) { throw new IllegalArgumentException ("Capacity must be positive." ); } this .capacity = capacity; cache = new HashMap <>(); freqMap = new TreeMap <>(); } public int get (int key) { if (!cache.containsKey(key)) { return -1 ; } Node node = cache.get(key); updateFreq(node); return node.value; } public void put (int key, int value) { if (cache.containsKey(key)) { Node node = cache.get(key); node.value = value; updateFreq(node); } else { Node node = new Node (key, value); if (cache.size() >= capacity) { LinkedList<Node> minList = freqMap.get(minFreq); Node removeNode = minList.pollFirst(); cache.remove(removeNode.key); if (minList.isEmpty()) { freqMap.remove(minFreq); } } cache.put(key, node); freqMap.computeIfAbsent(1 , k -> new LinkedList <>()).addLast(node); node.freq = 1 ; minFreq = 1 ; } } private void updateFreq (Node node) { int oldFreq = node.freq; LinkedList<Node> oldList = freqMap.get(oldFreq); oldList.remove(node); if (oldList.isEmpty()) { freqMap.remove(oldFreq); if (minFreq == oldFreq) { minFreq = freqMap.firstKey(); } } node.freq++; freqMap.computeIfAbsent(node.freq, k -> new LinkedList <>()).addLast(node); } }
—————-多线程并发题—————-
多线程交替打印数字 两个线程交替打印数字,一个线程打印奇数,另一个线程打印偶数,直到100。
使用synchronized实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class PrintOddEven { private final Object lock = new Object (); private int number = 1 ; public void printOdd () { synchronized (lock) { while (number < 100 ) { if (number % 2 == 0 ) { try { lock.wait(); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } else { System.out.println(Thread.currentThread().getName() + ": " + number); number++; lock.notify(); } } } } public void printEven () { synchronized (lock) { while (number < 100 ) { if (number % 2 != 0 ) { try { lock.wait(); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } else { System.out.println(Thread.currentThread().getName() + ": " + number); number++; lock.notify(); } } } } public static void main (String[] args) { PrintOddEven poe = new PrintOddEven (); Thread t1 = new Thread (poe::printOdd, "Odd" ); Thread t2 = new Thread (poe::printEven, "Even" ); t1.start(); t2.start(); } }
使用ReentrantLock实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 import java.util.concurrent.locks.Condition;import java.util.concurrent.locks.ReentrantLock;class PrintOddEvenLock { private final ReentrantLock lock = new ReentrantLock (); private final Condition condition = lock.newCondition(); private int number = 1 ; public void printOdd () { lock.lock(); try { while (number < 100 ) { if (number % 2 == 0 ) { condition.await(); } else { System.out.println(Thread.currentThread().getName() + ": " + number); number++; condition.signal(); } } } catch (InterruptedException e) { Thread.currentThread().interrupt(); } finally { lock.unlock(); } } public void printEven () { lock.lock(); try { while (number < 100 ) { if (number % 2 != 0 ) { condition.await(); } else { System.out.println(Thread.currentThread().getName() + ": " + number); number++; condition.signal(); } } } catch (InterruptedException e) { Thread.currentThread().interrupt(); } finally { lock.unlock(); } } public static void main (String[] args) { PrintOddEvenLock poe = new PrintOddEvenLock (); Thread t1 = new Thread (poe::printOdd, "Odd" ); Thread t2 = new Thread (poe::printEven, "Even" ); t1.start(); t2.start(); } }
使用Semaphore实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 import java.util.concurrent.Semaphore;class PrintOddEvenSemaphore { private final Semaphore oddSemaphore = new Semaphore (1 ); private final Semaphore evenSemaphore = new Semaphore (0 ); private int number = 1 ; public void printOdd () { try { while (number < 100 ) { oddSemaphore.acquire(); System.out.println(Thread.currentThread().getName() + ": " + number); number++; evenSemaphore.release(); } } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } public void printEven () { try { while (number < 100 ) { evenSemaphore.acquire(); System.out.println(Thread.currentThread().getName() + ": " + number); number++; oddSemaphore.release(); } } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } public static void main (String[] args) { PrintOddEvenSemaphore poe = new PrintOddEvenSemaphore (); Thread t1 = new Thread (poe::printOdd, "Odd" ); Thread t2 = new Thread (poe::printEven, "Even" ); t1.start(); t2.start(); } }
多线程按顺序打印ABC 三个线程按顺序打印ABC,重复10次。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 public class 线程交替打印字母_PrintABC { private static final Object object = new Object (); private static final int rounds = 3 ; private static int runNum = 0 ; private static final int max = 3 * rounds; private static void printA () { synchronized (object) { while (runNum < max) { if (runNum % 3 == 0 ) { System.out.println(Thread.currentThread().getName() + " " + runNum + ":A" ); runNum++; object.notifyAll(); } else { try { object.wait(); } catch (Exception e) { Thread.currentThread().interrupt(); } } } } } private static void printB () { synchronized (object) { while (runNum < max) { if (runNum % 3 == 1 ) { System.out.println(Thread.currentThread().getName() + " " + runNum + ":B" ); runNum++; object.notifyAll(); } else { try { object.wait(); } catch (Exception e) { Thread.currentThread().interrupt(); } } } } } private static void printC () { synchronized (object) { while (runNum < max) { if (runNum % 3 == 2 ) { System.out.println(Thread.currentThread().getName() + " " + runNum + ":C" ); runNum++; object.notifyAll(); } else { try { object.wait(); } catch (Exception e) { Thread.currentThread().interrupt(); } } } } } public static void main (String[] args) { Thread threadA = new Thread (线程交替打印字母_PrintABC::printA, "线程A" ); Thread threadB = new Thread (线程交替打印字母_PrintABC::printB, "线程B" ); Thread threadC = new Thread (线程交替打印字母_PrintABC::printC, "线程C" ); threadA.start(); threadB.start(); threadC.start(); } }
模拟死锁 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class DeadLockDemo2 { private static final Object objectA = new Object (); private static final Object objectB = new Object (); public static void main (String[] args) { Thread thread1 = new Thread (new MyTask (objectA, objectB), "Thread 1" ); Thread thread2 = new Thread (new MyTask (objectB, objectA), "Thread 2" ); thread1.start(); thread2.start(); } static class MyTask implements Runnable { private final Object firstResource; private final Object secondResource; public MyTask (Object objectA, Object objectB) { this .firstResource = objectA; this .secondResource = objectB; } @Override public void run () { System.out.println(Thread.currentThread().getName() + "获取第一个资源" ); synchronized (firstResource) { System.out.println(Thread.currentThread().getName() + "已获取第一个资源" ); try { Thread.sleep(100 ); } catch (InterruptedException e) { throw new RuntimeException (e); } System.out.println(Thread.currentThread().getName() + "获取第二个资源" ); synchronized (secondResource) { System.out.println(Thread.currentThread().getName() + "已获取第二个资源" ); } } } } }
模拟消息队列 使用阻塞队列实现生产者消费者问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import java.util.concurrent.ArrayBlockingQueue;import java.util.concurrent.BlockingQueue;class ProducerConsumer { private static final int CAPACITY = 10 ; private final BlockingQueue<Integer> queue = new ArrayBlockingQueue <>(CAPACITY); public void produce () throws InterruptedException { int value = 0 ; while (true ) { queue.put(value); System.out.println("Produced: " + value); value++; } } public void consume () throws InterruptedException { while (true ) { int value = queue.take(); System.out.println("Consumed: " + value); } } public static void main (String[] args) { ProducerConsumer pc = new ProducerConsumer (); Thread producer = new Thread (() -> { try { pc.produce(); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } }); Thread consumer = new Thread (() -> { try { pc.consume(); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } }); producer.start(); consumer.start(); } }
哲学家进餐问题 使用信号量解决哲学家进餐问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 class Philosopher implements Runnable { private final Semaphore leftChopstick; private final Semaphore rightChopstick; private final int philosopherNumber; public Philosopher (int philosopherNumber, Semaphore leftChopstick, Semaphore rightChopstick) { this .philosopherNumber = philosopherNumber; this .leftChopstick = leftChopstick; this .rightChopstick = rightChopstick; } @Override public void run () { try { while (true ) { think(); pickUpChopsticks(); eat(); putDownChopsticks(); } } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } private void think () throws InterruptedException { System.out.println("Philosopher " + philosopherNumber + " is thinking." ); Thread.sleep((long ) (Math.random() * 1000 )); } private void pickUpChopsticks () throws InterruptedException { leftChopstick.acquire(); rightChopstick.acquire(); System.out.println("Philosopher " + philosopherNumber + " picked up chopsticks." ); } private void eat () throws InterruptedException { System.out.println("Philosopher " + philosopherNumber + " is eating." ); Thread.sleep((long ) (Math.random() * 1000 )); } private void putDownChopsticks () { leftChopstick.release(); rightChopstick.release(); System.out.println("Philosopher " + philosopherNumber + " put down chopsticks." ); } } public class 哲学家进餐问题 extends Thread { public static void main (String[] args) throws InterruptedException { int numberOfPhilosophers = 5 ; Semaphore[] chopsticks = new Semaphore [numberOfPhilosophers]; for (int i = 0 ; i < numberOfPhilosophers; i++) { chopsticks[i] = new Semaphore (1 ); } Thread[] philosophers = new Thread [numberOfPhilosophers]; for (int i = 0 ; i < numberOfPhilosophers; i++) { Semaphore leftChopstick = chopsticks[i]; Semaphore rightChopstick = chopsticks[(i + 1 ) % numberOfPhilosophers]; philosophers[i] = new Thread (new Philosopher (i, leftChopstick, rightChopstick), "Philosopher " + i); philosophers[i].start(); } for (Thread philosopher : philosophers) { philosopher.join(); } } }
使用CyclicBarrier实现多线程任务 使用CyclicBarrier实现多个线程分段执行任务,每个线程打印自己的任务完成后,等待其他线程到达,然后继续下一段任务。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import java.util.concurrent.BrokenBarrierException;import java.util.concurrent.CyclicBarrier;class CyclicBarrierExample { private static final int THREAD_COUNT = 3 ; private static final CyclicBarrier barrier = new CyclicBarrier (THREAD_COUNT, () -> System.out.println("All threads completed a phase." )); public static void main (String[] args) { for (int i = 0 ; i < THREAD_COUNT; i++) { new Thread (new Task (), "Thread-" + i).start(); } } static class Task implements Runnable { @Override public void run () { try { for (int i = 1 ; i <= 3 ; i++) { System.out.println(Thread.currentThread().getName() + " completed phase " + i); barrier.await(); } } catch (InterruptedException | BrokenBarrierException e) { Thread.currentThread().interrupt(); } } } }
使用CountDownLatch实现任务协调 使用CountDownLatch等待多个线程完成任务后再继续主线程执行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import java.util.concurrent.CountDownLatch;class CountDownLatchExample { private static final int THREAD_COUNT = 3 ; private static final CountDownLatch latch = new CountDownLatch (THREAD_COUNT); public static void main (String[] args) { for (int i = 0 ; i < THREAD_COUNT; i++) { new Thread (new Task (), "Thread-" + i).start(); } try { latch.await(); System.out.println("All threads have finished. Main thread continues." ); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } static class Task implements Runnable { @Override public void run () { try { System.out.println(Thread.currentThread().getName() + " is working." ); Thread.sleep((long ) (Math.random() * 1000 )); System.out.println(Thread.currentThread().getName() + " has finished." ); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } finally { latch.countDown(); } } } }
使用Exchanger实现线程间数据交换 使用Exchanger实现两个线程交换数据。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import java.util.concurrent.Exchanger;class ExchangerExample { private static final Exchanger<String> exchanger = new Exchanger <>(); public static void main (String[] args) { new Thread (() -> { try { String data = "Data from Thread A" ; System.out.println("Thread A is exchanging: " + data); String receivedData = exchanger.exchange(data); System.out.println("Thread A received: " + receivedData); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } }, "Thread A" ).start(); new Thread (() -> { try { String data = "Data from Thread B" ; System.out.println("Thread B is exchanging: " + data); String receivedData = exchanger.exchange(data); System.out.println("Thread B received: " + receivedData); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } }, "Thread B" ).start(); } }
拓展:实现和指定的线程交换数据
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class ExchangerRegistry { private static final ConcurrentHashMap<String, Exchanger<String>> exchangers = new ConcurrentHashMap <>(); public static Exchanger<String> getExchanger (String threadName, String targetThreadName) { String key = generateKey(threadName, targetThreadName); return exchangers.computeIfAbsent(key, k -> new Exchanger <>()); } private static String generateKey (String threadName, String targetThreadName) { return threadName.compareTo(targetThreadName) < 0 ? threadName + "-" + targetThreadName : targetThreadName + "-" + threadName; } } class ExchangerExample { public static void main (String[] args) { Thread threadA = new Thread (() -> exchangeData("ThreadB" , "Data-A" ), "ThreadA" ); Thread threadB = new Thread (() -> exchangeData("ThreadA" , "Data-B" ), "ThreadB" ); Thread threadC = new Thread (() -> exchangeData("ThreadD" , "Data-C" ), "ThreadC" ); Thread threadD = new Thread (() -> exchangeData("ThreadC" , "Data-D" ), "ThreadD" ); threadA.start(); threadB.start(); threadC.start(); threadD.start(); } private static void exchangeData (String targetThreadName, String dataToSend) { String threadName = Thread.currentThread().getName(); Exchanger<String> exchanger = ExchangerRegistry.getExchanger(threadName, targetThreadName); try { System.out.println(threadName + " is exchanging: " + dataToSend); String receivedData = exchanger.exchange(dataToSend); System.out.println(threadName + " received: " + receivedData); } catch (InterruptedException e) { Thread.currentThread().interrupt(); } } }
——————数学相关——————
两数之和 在数组中找到两个数,使它们的和等于给定的数。
1 2 3 4 5 6 7 8 9 10 11 public int [] twoSum(int [] nums, int target) { Map<Integer, Integer> map = new HashMap <>(); for (int i = 0 ; i < nums.length; i++) { int complement = target - nums[i]; if (map.containsKey(complement)) { return new int [] { map.get(complement), i }; } map.put(nums[i], i); } throw new IllegalArgumentException ("No two sum solution" ); }
两数之和 II 在一个排序列表中找到两个数,使它们的和等于给定的数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int [] twoSum(int [] numbers, int target) { int left = 0 , right = numbers.length - 1 ; while (left < right) { int sum = numbers[left] + numbers[right]; if (sum == target) { return new int [] { left + 1 , right + 1 }; } else if (sum < target) { left++; } else { right--; } } throw new IllegalArgumentException ("No two sum solution" ); }
快乐数 判断一个数是否为快乐数,即反复将每个位的数字平方求和,最终会得到1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public boolean isHappy (int n) { Set<Integer> seenNumbers = new HashSet <>(); while (n != 1 && !seenNumbers.contains(n)) { seenNumbers.add(n); n = getSumOfSquares(n); } return n == 1 ; } private int getSumOfSquares (int num) { int sum = 0 ; while (num > 0 ) { int digit = num % 10 ; sum += digit * digit; num /= 10 ; } return sum; }
罗马数字转整数 将罗马数字转换为整数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int romanToInt (String s) { Map<Character, Integer> roman = new HashMap <>(); roman.put('I' , 1 ); roman.put('V' , 5 ); roman.put('X' , 10 ); roman.put('L' , 50 ); roman.put('C' , 100 ); roman.put('D' , 500 ); roman.put('M' , 1000 ); int sum = 0 ; for (int i = 0 ; i < s.length(); i++) { int current = roman.get(s.charAt(i)); int next = (i + 1 < s.length()) ? roman.get(s.charAt(i + 1 )) : 0 ; if (current < next) { sum -= current; } else { sum += current; } } return sum; }
整数反转 给你一个32位的有符号的int类型的数字,将数字上的每一位进行反转。
1 2 3 4 5 6 7 8 9 public int reverseInt (int x) { int rev = 0 ; while (x != 0 ) { int pop = x % 10 ; x /= 10 ; rev = rev * 10 + pop; } return rev; }
————–滑动窗口、动归————–
爬楼梯 1 2 3 4 5 6 7 8 9 10 public int climbStairs (int n) { if (n <= 2 ) return n; int [] dp = new int [n + 1 ]; dp[1 ] = 1 ; dp[2 ] = 2 ; for (int i = 3 ; i <= n; i++) { dp[i] = dp[i - 1 ] + dp[i - 2 ]; } return dp[n]; }
1 2 3 4 5 6 7 8 9 10 11 12 public int lengthOfLIS (int [] nums) { if (nums == null || nums.length == 0 ) return 0 ; int [] dp = new int [nums.length]; int len = 0 ; for (int num : nums) { int i = Arrays.binarySearch(dp, 0 , len, num); if (i < 0 ) i = -(i + 1 ); dp[i] = num; if (i == len) len++; } return len; }
能否组成顺子 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Shunzi { public static boolean isShunzi (int [] places) { if (places == null || places.length == 0 ) { return false ; } Arrays.sort(places); int zeroCount = 0 ; for (int num : places) { if (num == 0 ) { zeroCount++; } } int gapCount = 0 ; for (int i = zeroCount; i < places.length - 1 ; i++) { if (places[i] == places[i + 1 ]) { return false ; } gapCount += places[i + 1 ] - places[i] - 1 ; } return gapCount <= zeroCount; } public static void main (String[] args) { int [] test1 = {1 , 2 , 3 , 4 , 5 }; int [] test2 = {0 , 2 , 3 , 4 , 5 }; int [] test3 = {1 , 0 , 0 , 4 , 5 }; int [] test4 = {0 , 0 , 0 , 0 , 0 }; int [] test5 = {1 , 2 , 4 , 5 , 6 }; int [] test6 = {9 , 10 , 11 , 12 , 13 }; int [] test7 = {0 , 2 , 4 , 6 , 7 }; System.out.println(isShunzi(test1)); System.out.println(isShunzi(test2)); System.out.println(isShunzi(test3)); System.out.println(isShunzi(test4)); System.out.println(isShunzi(test5)); System.out.println(isShunzi(test6)); System.out.println(isShunzi(test7)); } }
最长公共前缀 找到字符串数组中的最长公共前缀。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static String getLongestPrefix (String[] strs) { if (strs == null || strs.length == 0 ) return "" ; String prefix = strs[0 ]; for (String str : strs) { while (!str.startsWith(prefix)) { prefix = prefix.substring(0 , prefix.length() - 1 ); } } return prefix; } public static String getLongestPrefix2 (String[] strs) { if (strs.length == 0 ) return "" ; String prefix = strs[0 ]; for (int i = 1 ; i < strs.length; i++) { while (strs[i].indexOf(prefix) != 0 ) { prefix = prefix.substring(0 , prefix.length() - 1 ); if (prefix.isEmpty()) return "" ; } } return prefix; }
最长递增子串的长度
递增子串:每个相邻 的数字之差为1,例如”1,2,3,4,5”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static int lengthOfCSQ (int [] nums) { if (nums == null || nums.length == 0 )return 0 ; int max = 1 , cur = 1 ; for (int i = 1 ; i < nums.length; i++) { if (nums[i] == nums[i - 1 ] + 1 ) { cur++; } else { max = Math.max(max, cur); cur = 1 ; } } max = Math.max(max, cur); return max; }
最长递增子序列的长度
递增子序列:不考虑前后数字是否相邻,只要是递增的就行,例如”1,…,4,9,…,10,…,17”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int lengthOfNCSQ (int [] nums) { if (nums == null || nums.length == 0 ) return 0 ; int n = nums.length; int [] dp = new int [n]; Arrays.fill(dp, 1 ); int max = 1 ; for (int i = 1 ; i < n; i++) { for (int j = 0 ; j < i; j++) { if (nums[i] > nums[j]) { dp[i] = Math.max(dp[i], dp[j] + 1 ); } } max = Math.max(max, dp[i]); } return max; }
最大子数组和 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class MaxSubArray { public static int maxSubArray (int [] nums) { for (int i = 1 ; i < nums.length; i++) { nums[i] = nums[i] + Math.max(0 , nums[i - 1 ]); } System.out.println("动规结果:" + Arrays.toString(nums)); return Arrays.stream(nums).max().getAsInt(); } public static int maxSubArray2 (int [] nums) { int pre = 0 , res = nums[0 ]; for (int num : nums) { pre = Math.max(pre + num, num); res = Math.max(pre, res); } return res; } public static void main (String[] args) { int [] nums = {-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 }; System.out.println(maxSubArray2(nums)); } }
最大连续子数组和 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class MaxContinuousSubArray { public static int maxSubArray (int [] nums) { int cur = nums[0 ], max = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { cur = Math.max(nums[i], cur + nums[i]); max = Math.max(max, cur); } return max; } public static void main (String[] args) { int [] nums = {-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 }; System.out.println(maxSubArray(nums)); } }
旋转数组 给定一个数组,将数组中的元素向右移动 k 个位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public void rotate (int [] nums, int k) { k %= nums.length; reverse(nums, 0 , nums.length - 1 ); reverse(nums, 0 , k - 1 ); reverse(nums, 0 , nums.length - 1 ); } private void reverse (int [] nums, int start, int end) { while (start < end) { int temp = nums[start]; nums[start] = nums[end]; nums[end] = temp; start++; end--; } }
搜索旋转排序数组 在旋转排序数组中查找一个特定的元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int search (int [] nums, int target) { int left = 0 , right = nums.length - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) return mid; if (nums[left] <= nums[mid]) { if (nums[left] <= target && target < nums[mid]) { right = mid - 1 ; } else { left = mid + 1 ; } } else { if (nums[mid] < target && target <= nums[right]) { left = mid + 1 ; } else { right = mid - 1 ; } } } return -1 ; }
是否是回文数 判断一个整数是否是回文数,即正读和反读都一样。
1 2 3 4 5 6 7 8 9 10 11 public boolean isPalindrome (int x) { if (x < 0 || (x % 10 == 0 && x != 0 )) { return false ; } int revertedNumber = 0 ; while (x > revertedNumber) { revertedNumber = revertedNumber * 10 + x % 10 ; x /= 10 ; } return x == revertedNumber || x == revertedNumber / 10 ; }
回文串判断 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 private static String getString () { StringBuilder sb = new StringBuilder (); for (char c : str.toCharArray()) { if (Character.isLetterOrDigit(c)) { sb.append(Character.toLowerCase(c)); } } retrun sb.toString(); } public static boolean isPalindrome (String str) { str = getString(str); int left = 0 ; int right = str.length() - 1 ; while (left < right) { if (str.charAt(left) != str.charAt(right)) { return false ; } left++; right--; } return true ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public static String longestPalindrome (String s) { if (s == null || s.isEmpty()) return "" ; int start = 0 , end = 0 ; for (int i = 0 ; i < s.length(); i++) { int len1 = expandAroundCenter(s, i, i); int len2 = expandAroundCenter(s, i, i + 1 ); int len = Math.max(len1, len2); if (end - start < len) { start = i - (len - 1 ) / 2 ; end = i + len / 2 ; } } return s.substring(start, end + 1 ); } private static int expandAroundCenter (String s, int left, int right) { while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) { left--; right++; } return right - left - 1 ; }
最长回文子串的长度 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public static int longestPalindromeLength (String s) { if (s == null || s.isEmpty()) return 0 ; int max = 0 ; for (int i = 0 ; i < s.length(); i++) { int len1 = expandAroundCenter(s, i, i); int len2 = expandAroundCenter(s, i, i + 1 ); max = Math.max(max, Math.max(len1, len2)); } return max; } private static int expandAroundCenter (String s, int left, int right) { while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) { left--; right++; } return right - left - 1 ; }
最长回文子序列的长度 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public static int longestPalindromeSubseqLength (String s) { if (s == null || s.isEmpty()) return 0 ; int n = s.length(); int [][] dp = new int [n][n]; for (int i = 0 ; i < n; i++) { dp[i][i] = 1 ; } for (int len = 2 ; len <= n; len++) { for (int i = 0 ; i <= n - len; i++) { int j = i + len - 1 ; if (s.charAt(i) == s.charAt(j)) { dp[i][j] = dp[i + 1 ][j - 1 ] + 2 ; } else { dp[i][j] = Math.max(dp[i + 1 ][j], dp[i][j - 1 ]); } } } return dp[0 ][n - 1 ]; }
示例 1:
1 2 3 输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
1 2 3 输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
1 2 3 4 输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int lengthOfLongestSubstring (String s) { if (s.length() == 0 || s == null ) return 0 ; Set<Character> set = new HashSet <>(); int left = 0 , right = 0 ; int max = 0 ; while (right < s.length()) { char ch = s.charAt(right); if (!set.contains(ch)) { set.add(ch); right++; max = Math.max(max, right - left); } else { set.remove(s.charAt(left)); left++; } } return max; }
1 2 3 4 5 6 7 8 9 10 11 12 public double findMedianSortedArrays (int [] nums1, int [] nums2) { int [] arr = IntStream.concat(Arrays.stream(nums1), Arrays.stream(nums2)).toArray(); Arrays.sort(arr); if (arr.length % 2 == 0 ){ return (double ) (arr[arr.length / 2 ] + arr[arr.length / 2 - 1 ]) / 2 ; } else { return arr[arr.length / 2 ]; } }